Как соединить резинку: Как сшить концы резинки | Швейный Советник

Как сшить концы резинки | Швейный Советник

Ателье, индивидуальный пошивКурсы шитьяРемонт швейной техникиСервисный центр AuroraСервисный центр BabylockСервисный центр BernetteСервисный центр BerninaСервисный центр BrotherСервисный центр ChaykaСервисный центр ElnaСервисный центр FamilyСервисный центр HusqvarnaСервисный центр JaguarСервисный центр JanomeСервисный центр JukiСервисный центр LeaderСервисный центр New HomeСервисный центр PfaffСервисный центр SingerСервисный центр ToyotaТкани

АнапаБалашихаБарнаулБийскБлаговещенскБрянскВеликий Новгород (Новгород)ВладимирВолгоградВологдаВоронежВсеволожскГатчинаЕкатеринбургЖуковскийИжевскИркутскКазаньКалининград (Кенигсберг)КемеровоКиргиз-МиякиКовровКомсомольск-на-АмуреКоролевКрасногорскКраснодарКрасноярскКурскЛипецкЛюберцыМахачкалаМоскваМуромМытищиНабережные ЧелныНальчикНевинномысскНижнекамскНижний НовгородНижний ТагилНовокузнецкНовороссийскНовосибирскНогинскОдинцовоОмскОрелПензаПермьПодольскПсковПятигорскРостов-на-ДонуСамараСанкт-ПетербургСаранскСтавропольСтарый ОсколСургутСыктывкарТамбовТверьТольяттиТомскТулаТюменьУральскУфаУхтаХабаровскХимкиЧебоксарыЧелябинскЧитаЩелковоЯрославль

Сначала популярныеПо алфавиту

Сейчас открыто

Выберите свой регион
Мы покажем вам актуальные контакты и цены на доставку

Закрыть

В каталогеВ мастер-классахВ обзорах

Как сшить концы резинки? Этот вопрос может возникнуть у тех, кто в первый раз шьет юбку или брюки на эластичной тесьме. Чтобы аккуратно соединить края, не увеличивая толщину пояса, рекомендуем воспользоваться нашим советом.

При выборе эластичной тесьмы необходимо обратить внимание на такие особенности:

• ширина резинки должна соответствовать модели, при этом деталь пояса должна быть на 2-5 мм шире, чем эластичная лента;
• для тёмных тканей можно брать любой цвет, а для светлых тканей лучше купить белую резинку;
• покупайте на 2-3 больше, чем обхват выбранного места (талия, объём над грудью, запястье и др.), и корректируйте длину резинки в ходе примерки.

Чтобы аккуратно стачать концы тесьмы понадобиться небольшой кусочек ткани и ножницы «зигзаг» (по возможности). Вначале сшивают пояс, оставляя отверстие для вдевания резинки. Затем эластичную тесьму вставляют внутрь с помощью булавки или специального приспособления. Два края вытаскивают наружу в отверстие и сшивают предложенным способом, а затем, расправив тесьму, отверстие в поясе зашивают.

Ход работы

Замерить длину детали, обернув сантиметр 1,5 раза вокруг резинки. Длина отрезка будет составлять тройную ширину резинки. Ширина прямоугольника 2,5-3 см. Припуски срезать ножницами «зигзаг».

Сколоть края резинки встык и наметать.

Обернуть место стыка лоскутом ткани и сколоть булавкой. Прострочить квадратом.

Края эластичной тесьмы соединены!

Задайте вопрос

Замыкание декоративной резинки в кольцо

08.04.2021

Товар по теме статьи

Как сделать декоративную резинку мы уже рассказывали в статьях Декоративная стёганая резинка из ткани изделия на бытовой машине и Декоративная стёганая резинка из ткани изделия на промышленной машине. В этой статье мы расскажем, как соединить резинку в кольцо, чтобы шов был незаметен.

Для образца потребуется прямоугольник ткани таких же размеров, как на фото ниже, где 8см —  припуск для удобства растягивания образца.

Сгибаем образец пополам вдоль и делаем разметку. Линии разметки 0.7 и 1см играют важную роль в дальнейшем пошиве, делаем их максимально точными. Припуски по 4см нужны, чтобы держать образец, когда мы прострачиваем резинку.

Стачиваем образец по горизонтальной линии разметки. Начало и конец горизонтальной строчки показаны на фото стрелками от вертикальной строчки-закрепки до второй строчки-закрепки.

Вставляем резинку в кулиску и лишь тогда делаем вертикальные строчки-закрепки. Где при этом расположены короткие края резинки показано на фото ниже. Если вы сделаете всё точно по образцу, дальнейший пошив не доставит сложностей.

Пристрачиваем резинку. Очень подробно об этом процессе рассказано в статье Декоративная стёганая резинка из ткани изделия на промышленной машине.

Затем срезаем излишки ткани по коротким сторонам образца вровень с короткими сторонами резинки.

Отворачиваем припуск только на одной короткой стороне образца на лицевую сторону и замыкаем резинку в кольцо.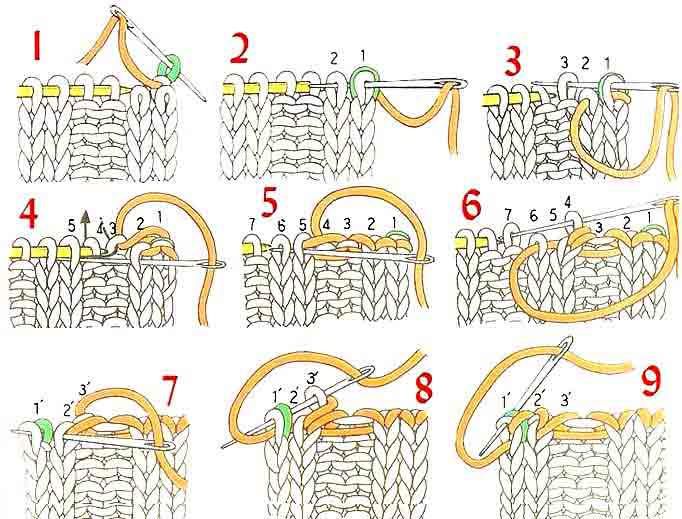

Важно! Припуск второй короткой стороны образца не отгибаем на лицевую сторону!

Стачиваем короткие стороны образца по линии разметки, равной 1см.

Подрезаем припуск до 3мм.

Вот так это выглядит с лицевой стороны.

Отгибаем припуск резинки на ту сторону, где голая резинка (без тканевого припуска) и фиксируем его строчкой.

А вот так это выглядит с лицевой стороны.

Примётываем припуск из ткани, согнув его точно пополам, вторая половина припуска располагается внутри.

Притачиваем припуск.

И с лицевой, и с изнаночной сторон образца удалось обойтись без утолщений шва и декоративная резинка чисто стачана в кольцо.

Стрелками показана последняя строчка.

Более детально весь процесс показан на видео, в котором объясняются все, даже самые мельчайшие, нюансы.

Статья подготовлена по материалам форума, автор мастер-класса OlgaLosss. Любое копирование и цитирование разрешено только с указанием источника и активной ссылки на эту статью.

Поделиться:

Теги

резинкастёжкаманжетадекоративнаязамыканиекольцоВсе теги

Товары

Полезные статьи по теме

Построение выкройки воротника-стойки для бомбера

22 марта 2021

Выкройка бомбера на 50-52 размер

19 марта 2021

Декоративная стёганая резинка из ткани изделия на бытовой машине

16 марта 2021

Декоративная стёганая резинка из ткани изделия на промышленной машине

16 марта 2021

Невозможная резиновая петля

Установлено: 6 января 2017 г.

Последнее обновление: … ; 1 ноября 2017 г .; 16 марта 2021 г .; 18 апр 2022 г.

4 августа 2017 г .:
Добавил обернутую картинку Рисунок 2 и
новый аргумент.

Этот документ

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/rubber-bands.html

Версия в формате PDF может быть добавлена ​​позже.

Частичный указатель дискуссионных заметок находится в

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/AREADME.html

Чего нельзя сделать с помощью цепочки из связанных резинок?

Предыдущий заголовок: Что можно сделать с помощью цепочки из связанных резинок?

(изменено 23 января 2017 г.)

Ниже представлены две картинки одной и той же цепочки из резинок. Вы, наверное, видите
сколько резинок и какую трехмерную форму принимает каждая резинка. Хотя
все полосы вышли из одного пакета, процесс связывания изменил 3-D
формы большинства из них. Одна форма отличается от остальных. Мы вернемся к
что ниже.

Предположим, вы крепко сжимаете две ленты на концах, по одной в каждой руке: тогда
многие движения, которые вы можете выполнять, не отпуская руки: встряхивание бинтов, растяжка
их (т. е. оттягивая концы дальше друг от друга), скручивая их, наматывая цепочку на
дверную ручку и дергая, наматывая их на подсвечник и т.д.
действие, которое вы можете выполнить, удерживая два конца, что вызовет резиновый
ленты развалиться, не порвавшись и не порезавшись? Если нет, то почему?

Довольно легко визуализировать изменения, сделанные путем добавления или удаления полос.

Вы, наверное, находите очевидным, что пока доступно больше резинок
их можно добавлять к тому или иному концу цепочки, сохраняя при этом узор
соединений. Можете ли вы визуализировать процесс добавления новой полосы в цепочку?
на любом конце?

Полосы соединены таким образом, что каждая полоса, кроме левой,
полоса имеет асимметричную форму: на левом конце последняя полоса образует простую
петля, в то время как на правом конце есть две петли, при этом следующая полоса идет
через них.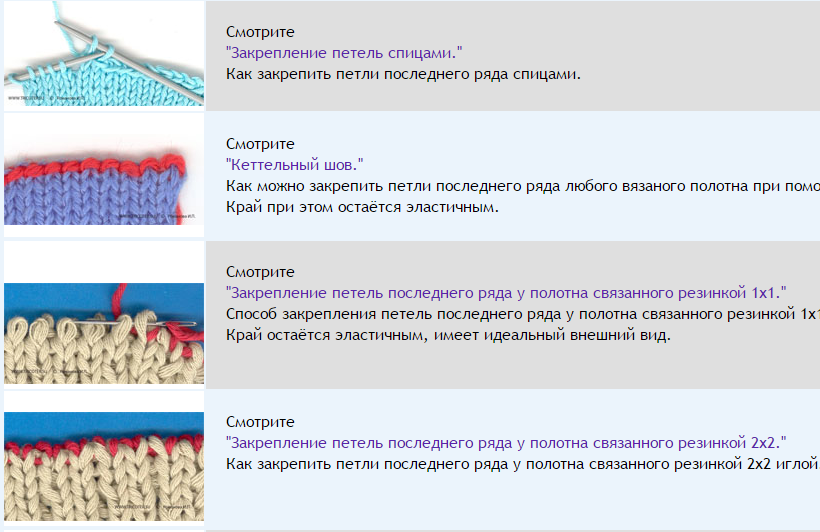

Чтобы сохранить шаблон связей на картинке, вам пришлось бы добавить новые
полосы к двум концам по-разному. Можете ли вы представить, что будет
требуется добавить полосу на любом конце? Какими должны быть процессы
ограничено, если вы хотите поддерживать регулярную схему соединений?

Как могла бы выглядеть цепочка, если бы вы добавили бэнды без сохранения
обычный узор? Можно ли производить чередующиеся типы
связь между группами?

Какие фигуры можно получить, соединив новую полосу с неконечной полосой в
цепь? Например. не могли бы вы сформировать форму «К» вместо линейной формы? Может ли
полосы должны быть связаны, чтобы сформировать форму ветвящегося дерева, с тремя ветвями, добавленными в
каждый узел?

Более сложный(?) вопрос:

Могут ли связанные резинки смыкаться, образуя петлю?

Можно ли соединить два конца цепи так же, как
пары соседних лент соединяются, т. е. проталкивая петлю на одном конце ленты
через другой конец ленты, а затем протягивая остальную часть ленты через петлю?
Это замкнет цепочку полос, чтобы сформировать большую петлю.

На рисунке 2 показано, что такое цепочка из резинок
растягивается вокруг другого объекта и соединяется вне поля зрения, образуя замкнутый контур
выглядел бы!

Если этого нельзя сделать, то почему?

Здесь представлено еще много примеров различных типов невозможности:

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/impossible.html

Можно ли обучить текущий механизм обучения ИИ различать вещи, которые
возможных из невозможных (хотя их можно описать или
изображен)?

Для основанных на статистике форм обучения (например, используемых в
Глубокое обучение), чья форма обучения дает полезные оценки вероятности,
когда-нибудь обнаружить, что что-то невозможно, или что
определенные свойства объекта или процесса овладевают другими свойствами посредством
этот конкретный объект или процесс невозможен. Это требует другого рода познавательной
механизм, о котором, насколько мне известно, современная нейронаука нам ничего не говорит.

Это потому, что модальные понятия «обязательно истинны».
и «невозможно» совершенно отличны от понятий очень высокого и
очень низкая степень вероятности, на которой может основываться применение
статистические доказательства.

Существуют средства для доказательства теорем на основе ИИ, которые могут определить, является ли та или иная формула правильной.
доказуема в рамках системы аксиом и правил для определенных классов формул.
Это требует, чтобы средство доказательства теорем включало в себя «метазнание» о своем собственном
операция. Доказать, что нет доказательства, длина которого меньше N шагов, можно
как правило, осуществляется путем полного перебора. Демонстрация того, что нет доказательств
любая длина обычно намного сложнее. Вопросы такого рода могут привести к
неразрешимость приводит к математике, логике и искусственному интеллекту.

Существуют ли также теоремы о неразрешимости, ожидающие доказательства относительно
механизмы человеческого мозга? Ответы могут зависеть от того, какие ресурсы доступны
вне мозга, т.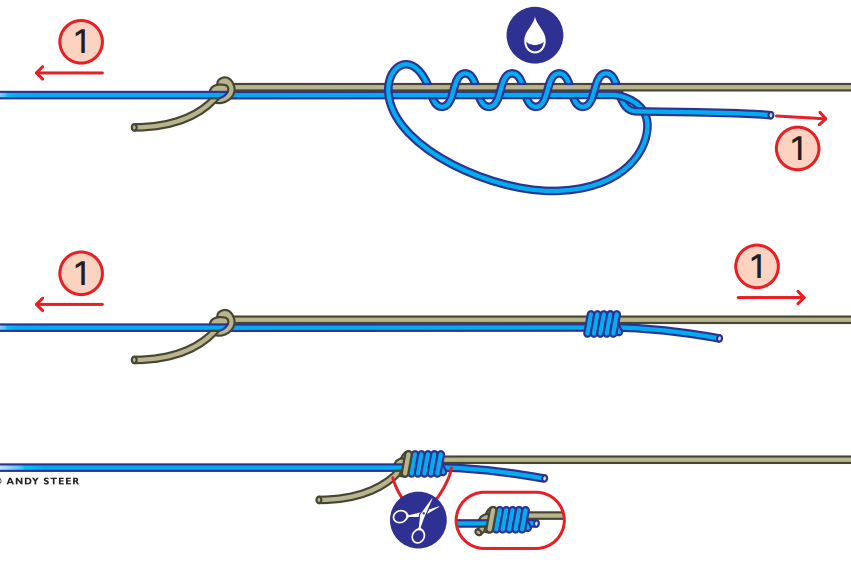 е. средства для рисования, такие как карандаш и бумага, или 3-D
структуры, которыми можно манипулировать для изучения возможных конфигураций.

Вопрос математикам:

Является ли эта невозможность замыкания цикла известной теоремой трехмерной топологии или особым
случай известной теоремы? Что за доказательство невозможности замкнуть петлю
соответствовали бы современным математическим стандартам строгости? Существуют ли повсеместно
согласованные стандарты? Как они оправдываются?

Как нематематикам может показаться очевидным, что замкнуть цикл невозможно?
(возможно, немного подумав). Я спросил нескольких, которые не заставили себя долго ждать.
решить это было невозможно, хотя им было нелегко сказать, почему нет?

Какие мозговые механизмы делают возможными такие процессы? Как они эволюционировали? Как
они развиваются у отдельных лиц? Они существуют только в мозгу людей с
математическая подготовка?

Зависят ли механизмы пространственного мышления, доступные отдельному мозгу?
на окружающую среду и возможности, которые она предоставляет для обучения делать различные
виды пространственного мышления (например, те, которые использовались древними
математики, сделавшие геометрические и топологические открытия задолго до
предпринимались попытки формализовать пространственные способы рассуждения)?

Почему невозможность трудно объяснить?

Какова роль предположения, что никакая часть резинки не может пройти через
через другую часть резинки?

Смежный вопрос: какой зрительный механизм или механизм рассуждения заставляет
можно обнаружить, что IF резинки бесконечно растягиваются
(чтобы различия в размерах и толщине не создавали препятствий) ЗАТЕМ :

а) всегда можно связать изолированную пару резинок с помощью
упомянутая процедура (производство двухзвенной цепи)?

(б) всегда можно удлинить такую ​​цепочку, связав новый изолированный
резинка к концевой ленте?

(c) такую ​​(линейную) цепь никогда нельзя преобразовать в замкнутую цепь
протолкнув петлю на одном конце ленты через другую, а затем потянув за
остальная часть первой полосы через свою петлю?

Я предполагаю, что любой, кто читает и понимает (с), согласится с тем, что
процесс невозможен, но большинство нематематиков (и некоторые математики)
будет трудно объяснить, почему. Если я ошибаюсь и это возможно, пожалуйста
дайте мне знать, как. Если можно, сделайте видео процесса или
последовательность снимков.

Интересный аргумент в пользу невозможности

В июле 2017 года я получил интересное предложение с изложением потенциального доказательства
невозможности замыкания цепи (без разрезания и соединения частей
резинка) от Лейлы Сломан

https://mathematics.stanford.edu/people/leila-sloman

и Дэвид Шерман (в то время оба аспиранты Стэнфордского университета)

Они предложили начать с наблюдения, что если петля замкнута как
намекает на рис. 2, его нельзя было «открыть» (без
разрезая и соединяя полосу), чтобы сформировать линейную цепочку вида
изображен на рисунке 1.

Я согласен, что это каким-то образом «кажется» невозможным, в отличие от
воспринимая невозможность запуска с разомкнутой цепью как на рисунке 1
и преобразование ее в замкнутую цепь без разрезания и соединения.

Краткое изложение их аргументов, как я понимаю:

Конфигурация, состоящая из замкнутой петли связанных резинок, не может быть
открылась, расстегнув одну из резинок, так как при попытке сделать это
закончит тем, что вернет эту полосу по кругу в то же место, где она началась.

Попробуйте визуализировать отмену одной из ссылок
изображен на рисунке 2.

Тот факт, что петлю нельзя отменить, необходимо строго доказать. Как
можно ли это сделать? Есть ли релевантная известная теорема об узлах?

Невозможный процесс против невозможной структуры

NB Я не говорю, что невозможна полная круговая цепочка
резинки к есть : просто невозможно изготовить
из набора имеющихся резинок без введения временной
разрыв в какой-либо из полос.

Если последняя полоса каким-то образом «выросла» на месте или полоса обрезана, зациклена как
требуется, а затем срез сросся так, что стык не виден, затем результат
может быть полной круговой цепочкой связанных резинок. Так что это не тип
объект , который здесь заявлен как невозможный, но тип процесса .

Справится ли любой существующий в настоящее время автоматизированный доказатель теорем?


Существует ли какой-либо автоматический доказатель теорем, который может сделать такое открытие?
описано выше и доказать невозможность? Я предполагаю, что все глубокое обучение
технология не имеет значения, так как она не дает (не может) знания о
что невозможно, или обязательно имеет место, или математические последствия.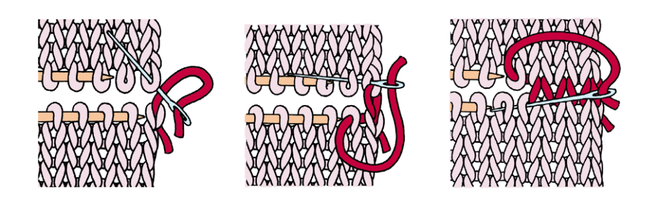 Это
потому что невозможность и необходимость не являются низкими и высокими крайностями
вероятность: это понятия в другом пространстве.

Многие аспекты евклидовой геометрии связаны не со статичными структурами
(несмотря на частое использование статических диаграмм), но с инвариантными чертами
процессы , которые создают или модифицируют структуры. Например, инвариант
аспекты площадей или изменения площадей треугольников как треугольной формы
(и/или положение, ориентация или размер) суммируются в теоремах о
площади плоских треугольников, как показано здесь:

Скрытые глубины Треугольника Квалиа (особенно их области).

Старые и новые доказательства суммы внутренних углов треугольника.

(Подробнее о скрытых глубинах треугольных квалиа.)

Отдельный файл
Теорема о сумме треугольников обсуждает способы
демонстрируя, что изменение размера или формы плоского треугольника не
изменить сумму внутренних углов.

Я подозреваю, что биологическая эволюция создала механизмы для (протоматематических?)
рассуждения о деформируемых структурах, которые не являются точно плоскими, и не
включать бесконечно тонкие или бесконечно длинные или совершенно прямые
линии, задолго до развития евклидовой геометрии.

Однако не все организмы, которые могут использовать такие математические рассуждения (например,
обезьяны чистят бананы?) знают, что они это делают, и могут обсуждать свои
рассуждая с другими. Это включает в себя довербальных человеческих малышей, как показано на рисунке.
в этом документе:

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/toddler-theorems.html

Метаморфогенез и теоремы для малышей: тематические исследования

Я думаю, что все это связано с тем, что Джеймс Гибсон классно назвал
восприятие «возможностей» (включая возможности и препятствия для возможных
действия), хотя я не знаю, замечал ли он когда-либо связь с
древние математические открытия. Насколько я знаю, он не смог указать
механизмы для обнаружения и рассуждения о аффордансах, за исключением нескольких
Особые случаи.

Джей Джей Гибсон,

Экологический подход к визуальному восприятию,

Хоутон Миффлин,
Бостон, Массачусетс,
1979 г.,

Предельный случай

Некоторые читатели могли заметить, что «теорема невозможности» также
относится к цепочке, состоящей только из одной резинки : она не может быть зациклена
с самим собой, чтобы создать «замкнутую» цепочку таким образом, чтобы ее можно было связать с другим
группа. Мне потребовалось пару недель, чтобы заметить это.

Пример предоставлен Норманом Мегиллом

9 сент. 2021 г.

После того, как я отправил вопрос о цепочке из резинок в «фом»
(Основы математики) дискуссионный список, Норман Мегилл (соавтор Metamath
http://us.metamath.org/) прислал мне это
изображение (воспроизведено здесь с его разрешения):

Он написал:

Хотя это не отвечает на ваш вопрос, это напомнило мне о простом трюке, который
очаровал детей (и, возможно, некоторых взрослых). Возможно, вы найдете его
занимательный.

Сначала вы держите резинку с одним концом петли в каждой руке и спрашиваете, как
чтобы соединить концы вместе, что, казалось бы, потребует прохождения
резинка через себя. Многие люди подумают, что это невозможно. Затем с
немного быстрых манипуляций, вы производите конфигурацию в прикрепленном файле
картина. После того, как резинка вернулась в нормальное состояние, некоторые люди все еще не могут
производите конфигурацию на картинке, и на них интересно смотреть
борьба.

Я не знаю, стандартный ли это трюк. Я наткнулся на него случайно, когда
несколько лет назад играл с резинкой.

Моей первой реакцией было: «Это просто». Я взял резинку и кружку — и не смог.
Затем я снова посмотрел на картинку и понял, что мне нужны два поворота, а не просто
один! Подробности оставляем читателю!

Топология для малышей

Математические способности человека, включающие способность замечать и описывать
пространственные возможности и невозможности, и рассуждать о них, вырастают из
способности, развившиеся намного раньше и (в некоторых случаях) общие с другими
разумные виды (например, белки, слоны, человекообразные обезьяны, птицы, строящие гнезда,
охота на млекопитающих). Похоже, что даже у довербальных человеческих малышей/гусениц есть
(нерефлексивные) способности к геометрическому и топологическому мышлению, такие как 17,5
месячный ребенок в этом видео:

http://www.cs.bham.ac.uk/research/projects/cogaff/movies/ijcai-17/small-pencil-vid.webm

В настоящее время я не думаю, что кто-либо знает, как эти способности обнаружить и сделать
использование пространственных возможностей, невозможностей и необходимости (еще один аспект
невозможности) эволюционировали или как способности реализуются в мозгу. Логика
основанные на автоматизированных средствах доказательства теорем делают что-то совершенно отличное от
рассуждения древних математиков, белок, малышей и т.д. Какие-то полусырые
идеи о том, как развивались некоторые из этих способностей (используя то, что Джеки Чаппелл и
я называю «метаконфигурированные геномы») можно найти здесь, включая короткое видео
объяснение части теории:

http://www.cs.bham.ac.uk/research/projects/cogaff/movies/meta-config

Способы использования резиновых лент в сочетании с (например) кусочками проволоки в петле

https://www. wikihow.com/Make-a-Rubber-Band-Necklace

СВЯЗАННЫЕ ДОКУМЕНТЫ

Этот документ является одним из многих примеров восприятия возможностей
и невозможности (включая геометрию, топологию и числа) в этой сети
сайт. Вот еще некоторые из них (включая уже упомянутые выше):

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/triangle-sum.html

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/trisect.html

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/triangle-theorem.html

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/impossible.html

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/torus.html

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/shirt.html

Еще одна задача для автоматизированных систем рассуждений — открыть/изобрести трехмерную модель.
онтология для объяснения/понимания воспринимаемых двумерных явлений:

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/nature-nurture-cube. html

Это часть вдохновленного Тьюрингом проекта метаморфогенеза:

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/meta-morphogenesis.html

Долгосрочный проект: указать машину рассуждений Супер-Тьюринга, способную
эти открытия и их объяснение:

http://www.cs.bham.ac.uk/research/projects/cogaff/misc/super-turing-geom.html

ССЫЛКИ И ССЫЛКИ (будут добавлены)

Поддерживается
Аарон Сломан

Школа компьютерных наук

Бирмингемский университет

Инструмент для изготовления браслетов EZ Looper Rubber Band

Сейчас:

2,45 доллара США

(пока отзывов нет)

Написать обзор

Инструмент для изготовления браслетов EZ Looper Rubber Band

Рейтинг
Обязательно

Выберите рейтинг1 звезда (худший)2 звезды3 звезды (средний)4 звезды5 звезд (лучший)

Имя
Обязательно

Электронная почта
Обязательно

Тема обзора
Требуется

Комментарии
Обязательно

Артикул:

ЭЗЛУПЕР

Наличие:

EZLOOPER, инструмент EZ Looper, устройство для изготовления браслетов из резинок, инструмент для i-cord, мини-ткацкий станок, крошечный ткацкий станок, ткацкий станок для пальцев, детские поделки, силиконовая резинка, силиконовые петли, EZ Looper, зажимы для браслетов, разноцветные резинки, крошечные резинки

• Описание

EZ Looper специально разработан с 6 штифтами для создания каучуковых браслетов от базовых до продвинутых за считанные минуты.