Какие фигуры правильные: Какие фигуры называют правильными — MicroArticles
Какие фигуры называют правильными — MicroArticles
Учеба
-> Среднее образование
| Автор: Крагель Татьяна Петровна | Добавлено: 2015-02-19
Многоугольник называют правильным, если у него равны стороны и углы . Примерно так определяются и правильные многогранники.
Выпуклый многогранник называется правильным, если его грани- равные правильные многоугольники и двухгранные углы при всех рёбрах равны между собой.
Правильных многоугольников бесконечно много. Правильных многогранников всего пять. По числу граней их называют тетраэдр (четырехгранник), гексаэдр (шестигранник или куб), октаэдр (восьмигранник), додекаэдр (двенадцатигранник) и икосаэдр (двадцатигранник).
То что каждый из них выпуклый, легко проверить экспериментально: подержите в руках каждую модель и прислоните ладонь к каждой грани фигуры. Вы убедились, что вся фигура оказалась по одну сторону от ладони? Касаясь любой грани ладонью и мысленно проведя через ладонь плоскость, вы увидите, что эта воображаемая плоскость нигде не разрежет ни одну из рассматриваемых фигур. Проверить равенство рёбер и плоских углов можно простым измерением с помощью линейки и транспортира.
Проверить равенство рёбер и плоских углов можно простым измерением с помощью линейки и транспортира.
Правильные многогранники обладают различными видами симметрии, поэтому в древности их называли «идеальными», «космическими» телами.
Правильные многогранники называют также Платоновыми телами хотя их знали пифагорейцы за несколько веков до Платона. В диалоге «Тимей» Платон связал их с четырьмя основными элементами. Он считал, что куб, тетраэдр, октаэдр, икосаэдр имеют форму корпускул земли, огня, воздуха и воды соответственно. Пятый же многогранник он считал моделью всей Вселенной.
Изучая многогранники, можно подсчитать, сколько у них граней, ребер и вершин.
Теория правильных многоугольников и многогранников – один из самых увлекательных и ярких разделов математики. Но закономерности, открытые математиками, удивительным образом связаны с симметрией живой и неживой природы – с формами различных кристаллов, точной формой вирусов, с современными теориями в физике, биологии и других областях знания.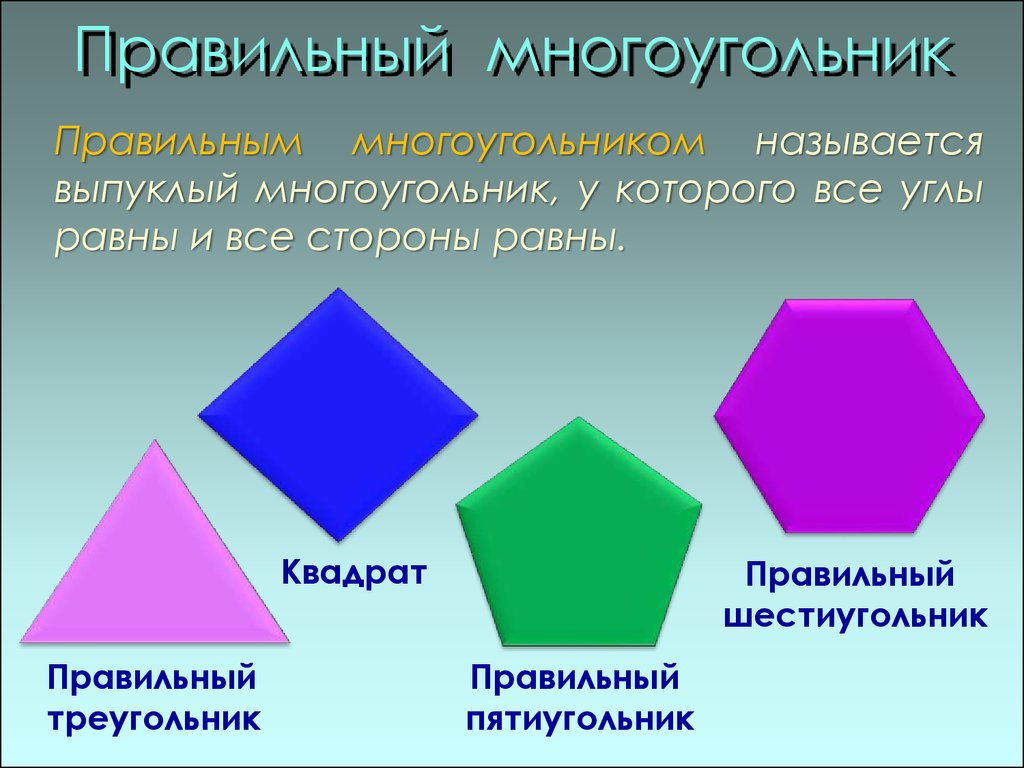 Так, например, вершины снежинки всегда образуют правильный шестиугольник, а хорошо знакомый нам куб природа реализовала в форме кристаллов поваренной соли.
Так, например, вершины снежинки всегда образуют правильный шестиугольник, а хорошо знакомый нам куб природа реализовала в форме кристаллов поваренной соли.
Правильные многогранники – самые выгодные фигуры. И природа этим широко пользуется. Например, скелет одноклеточного организма феодарии по форме напоминает икосаэдр.
Большинство феодарий живут на морской глубине и служат добычей коралловых рыбок. Но простейшее животное пытается себя защитить: из 12 вершин скелета выходят 12 полых игл. На концах игл находятся зубцы, делающие иглу еще более эффективной при защите.Чем же вызвана такая природная геометризация феодарий? Тем, по-видимому, что из всех многогранников с тем же числом граней именно икосаэдр имеет наибольший объем при наименьшей площади поверхности. Это свойство помогает морскому организму преодолевать давление водной толщи.
Интересно, что икосаэдр оказался в центре внимания биологов в их спорах относительно формы некоторых вирусов. Вирус не может быть совершенно круглым, как считалось раньше. Для того, чтобы определить его форму, брали разные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает такую же тень – икосаэдр.
Для того, чтобы определить его форму, брали разные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает такую же тень – икосаэдр.
Некоторые кристаллы имеют форму правильных многогранников. Например, монокристалл алюминиево-калиевых квасцов имеет форму октаэдра, кристаллы сернистого колчедана – форму додекаэдра, кристалл сурьменистого сернокислого натрия имеет форму тетраэдра, икосаэдр передает форму кристаллов бора.
1. Идеально правильные фигуры. Кристаллы
1. Идеально правильные фигуры
На рисунке 3 представлено несколько многогранников. Их очертания очень совершенны, как говорят, идеально правильны.
В чём заключается совершенность изображённых тел, заслужившая для них название идеально правильных?
Рис. 3. Многогранники: а – куб; б – октаэдр; в – два додекаэдра – слева ромбододекаэдр, справа пентагондодекаэдр; г – шестигранная призма; д – сочетание призмы с двумя шестигранными пирамидами.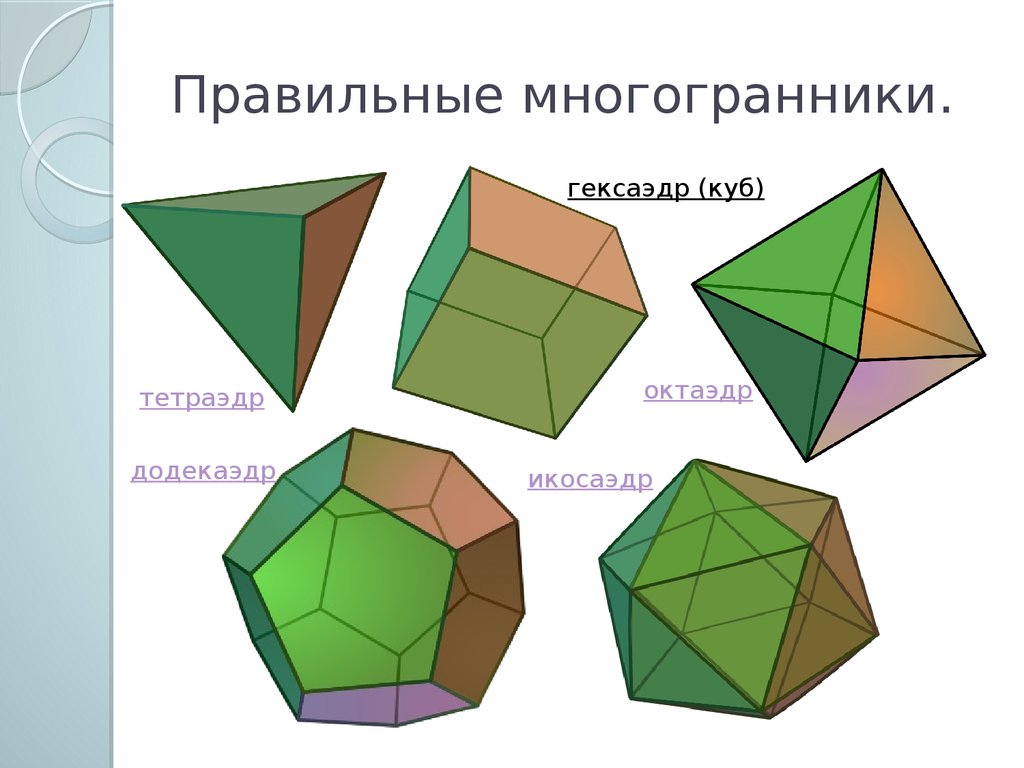
Многогранник, показанный на рисунке 3, а, называется кубом; у него 6 граней, 12 рёбер и 8 вершин. На рисунке 3, б показан октаэдр. Слово «окта» по-гречески означает восемь, окончание «эдр» означает грань, название «октаэдр» соответствует русскому слову восьмигранник; у октаэдра 6 вершин и 12 рёбер. На рисунке 3, в изображены два разных двенадцатигранника. Один из них называется ромбододекаэдром (приставка «ромбо» указывает на форму грани, «додека» значит двенадцать.) Все его грани, как видно из рисунка, имеют форму ромба. Подсчитывая число вершин и рёбер у додекаэдра, получим соответственно 14 и 24. Рядом изображён пентагондодекаэдр. У него также двенадцать граней, но грань имеет форму пентагона – пятиугольника («пента» – пять, «гон» – угол).
У перечисленных пока что фигур все грани имеют одну и ту же форму. У куба – это квадраты, у октаэдра – равносторонние треугольники, у додекаэдра – ромбы или пятиугольники.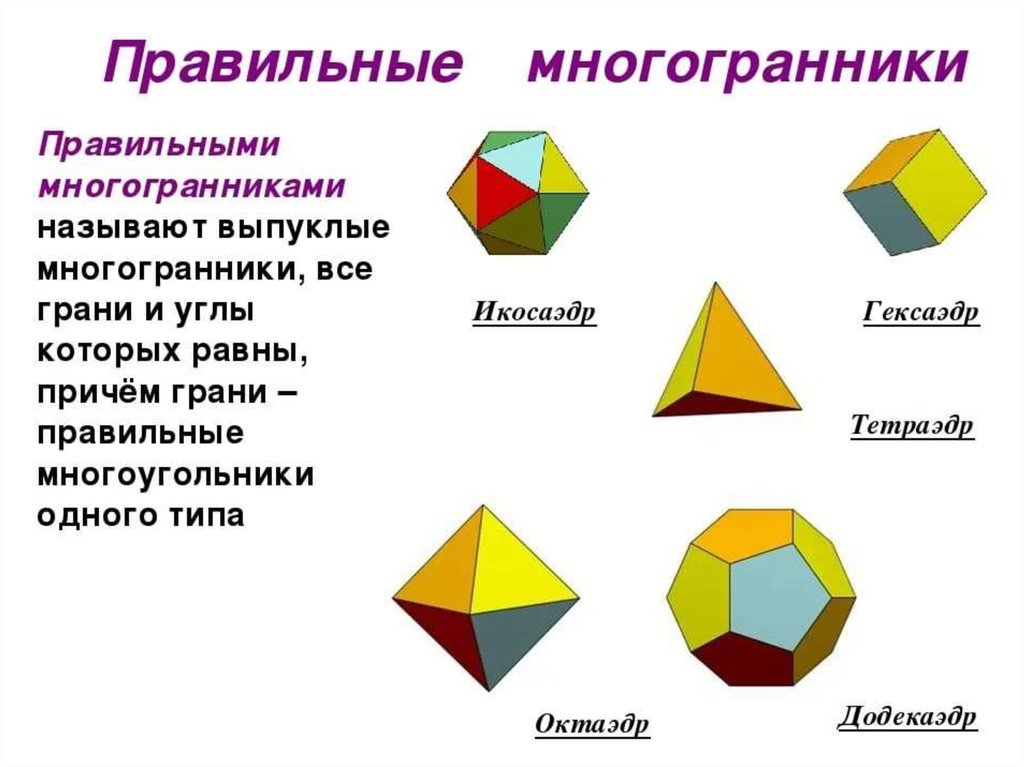
Эти правильные тела – самые простые. Но существуют и несколько более сложные формы. На рисунке 3, г изображена шестигранная призма. Два основания её – правильные шестиугольники, шесть боковых сторон – прямоугольники. Всего граней 8, рёбер 18 и вершин 12. Рядом (рис. 3, д) показана красивая фигура, состоящая из двух шестигранных пирамид и одной шестигранной призмы. У этого тела 30 рёбер, 14 вершин и 18 граней – 12 граней имеют форму равнобедренного треугольника и 6 прямоугольны.
Мы приводим числа вершин, рёбер и граней, чтобы обратить внимание читателя на одно интересное правило, установленное знаменитым петербургским академиком Леонардом Павловичем Эйлером: число рёбер равно сумме числа граней и вершин, уменьшенной на два. Действительно, имеем для куба 12 = 6 + 8 – 2; для октаэдра 12 = 8 + 6 – 2; для ромбододекаэдра 24 = 12 + 14 – 2; для шестигранной призмы 18 = 8 + 12 – 2; у фигуры на рисунке 3, д 30 = 18 + 14 – 2.
Фигуры, подобные описанным нами, можно выпилить из дерева или изготовить искусственно из какого-либо иного материала.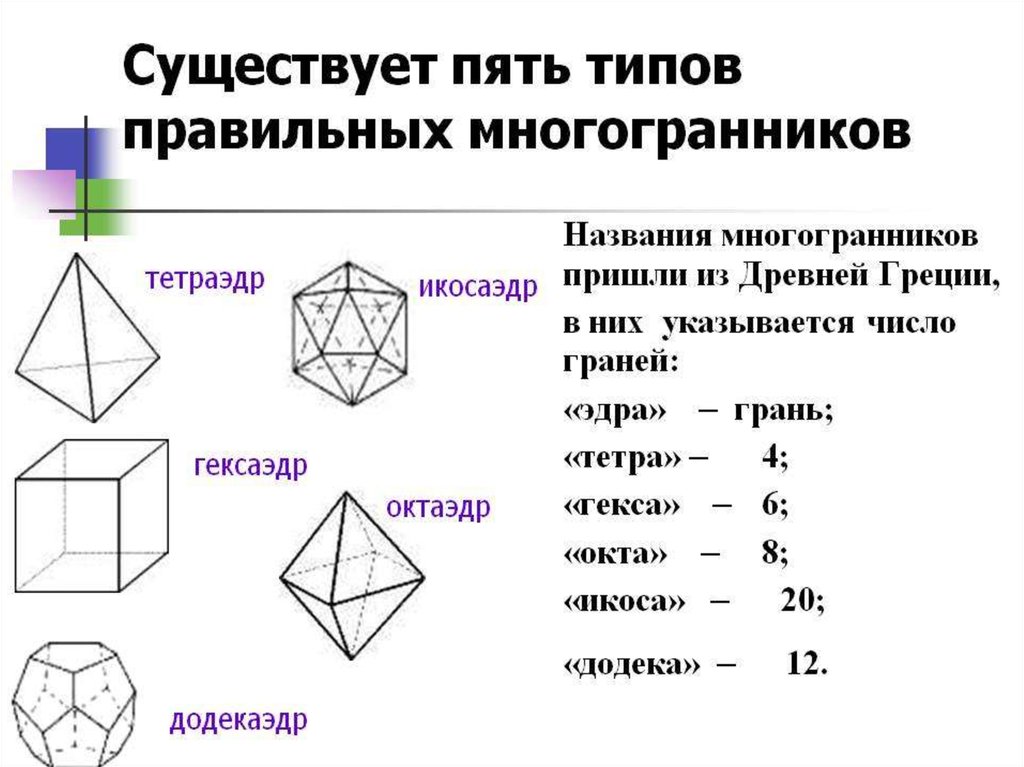 Замечательно, однако, то обстоятельство, что при некоторых предосторожностях (о которых мы будем говорить ниже, стр. 58) кристаллы вырастают в виде идеальных многогранников. В виде кубиков можно получить каменную соль. Алмаз находят в природе в виде октаэдров, а гранит – в виде ромбододекаэдров. Однако значительно чаще кристаллы принимают форму не простых, а сложных многогранников, имеющих несколько разных «сортов» граней. Например, кристаллы кварца довольно часто встречаются в виде только что описанных тел (рис. 3, д) с гранями двух сортов – прямоугольными и треугольными.
Замечательно, однако, то обстоятельство, что при некоторых предосторожностях (о которых мы будем говорить ниже, стр. 58) кристаллы вырастают в виде идеальных многогранников. В виде кубиков можно получить каменную соль. Алмаз находят в природе в виде октаэдров, а гранит – в виде ромбододекаэдров. Однако значительно чаще кристаллы принимают форму не простых, а сложных многогранников, имеющих несколько разных «сортов» граней. Например, кристаллы кварца довольно часто встречаются в виде только что описанных тел (рис. 3, д) с гранями двух сортов – прямоугольными и треугольными.
Калькулятор значащих цифр
Использование калькулятора
Сложение, вычитание, умножение и деление значащих цифр. Введите числа, экспоненциальное представление или электронное обозначение и выберите математический оператор. Калькулятор вычисляет и округляет ответ до правильного количества значащих цифр (сиг-фиг).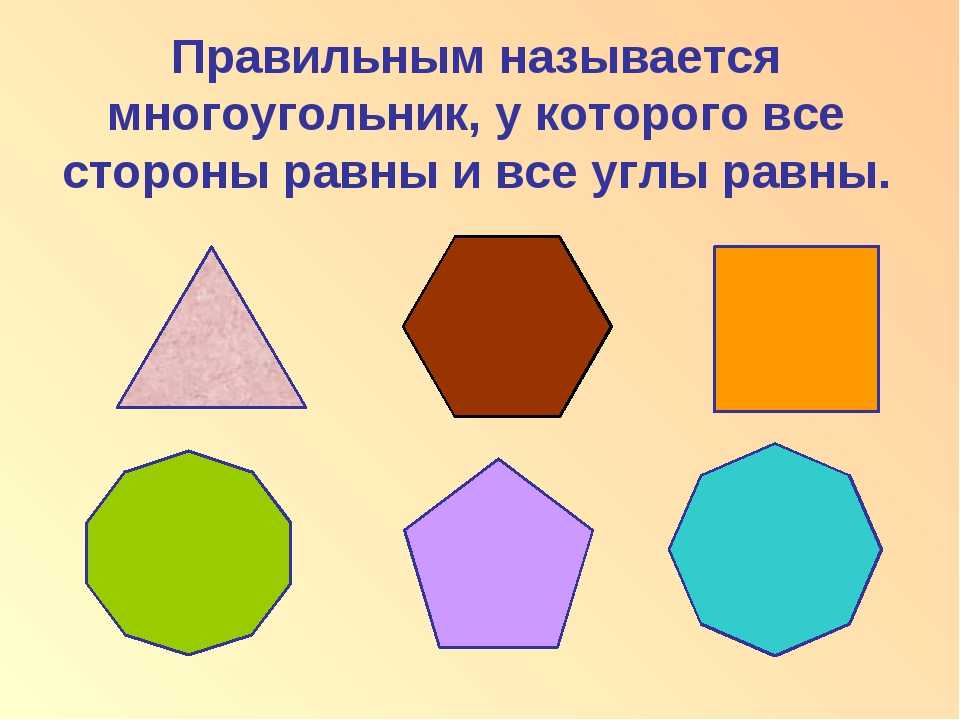 3 и 3,5e3.
3 и 3,5e3.
Подробнее о вычислениях со значащими цифрами читайте ниже.
Что такое значимые цифры?
Значащие цифры — это цифры числа, имеющие значение с точки зрения точности или прецизионности. Эти цифры предоставляют информацию о том, насколько точным может быть расчет или измерение.
Значащие цифры Правила
- Ненулевые цифры всегда значащие
- Нули между ненулевыми цифрами всегда значимы
- Ведущие нули никогда не являются значащими
- Нули в конце имеют значение, только если число содержит десятичную точку
Примеры значащих цифр
3
2, 6, 2
6
5, 2, 0, 0, 3, 8 04 3
7 , 8, 8
4
7, 8, 8, 0
5
7, 8, 8, 0, 0
Правила сложения и вычитания со значащими цифрами
- Найти позицию последней значащей цифры в наименее определенном числе
- Добавьте и/или вычтите числа в вашем расчете, как обычно
- Округлите ответ до наименее значимой позиции, которую вы нашли на шаге 1
Пример: сложение и вычитание со значащими цифрами
На одном из этапов лабораторного задания по химии «Приготовим латте» необходимо учитывать объем жидкости в латте.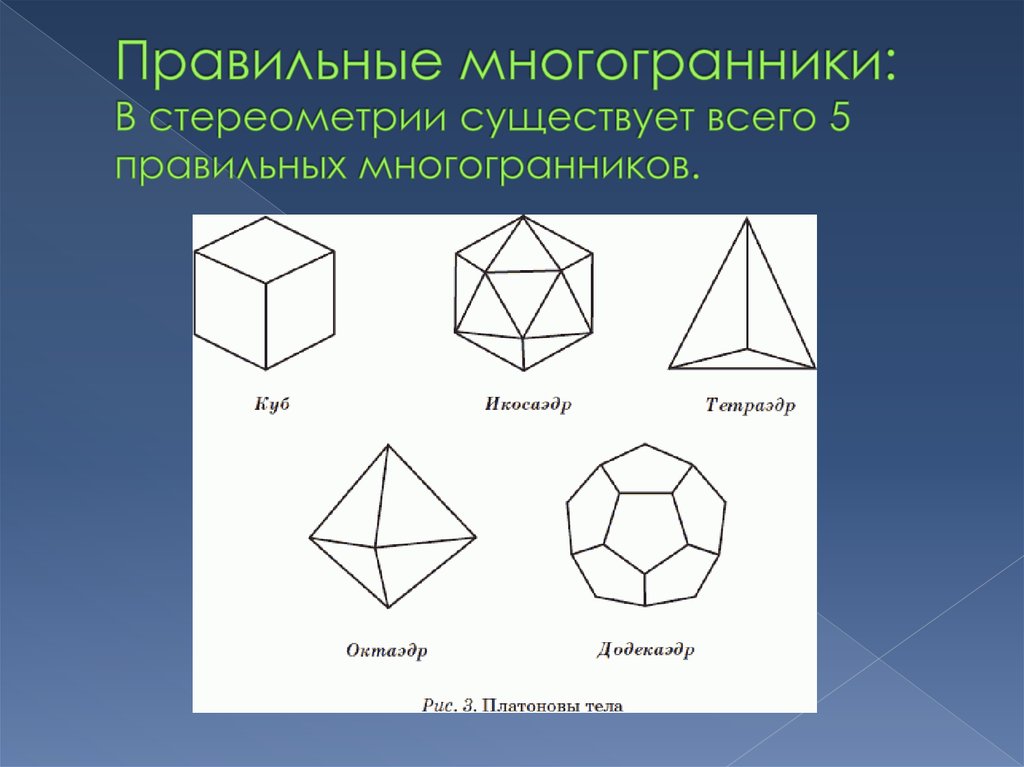
Вы начинаете с 7 унций. молока, а ваша эспрессо-машина использует 2,5 унции. воды, чтобы сделать 2 унции. шот эспрессо — остальные 0,5 унции. остается в шайбе для эспрессо. Наконец, ваш высокотехнологичный парогенератор для молока сообщает вам, сколько воды используется в процессе приготовления на пару, с точностью до 3 знаков после запятой.
Вы готовите эспрессо и видите, что у вас получились идеальные 2 унции. выстрелил. Вы пропариваете и вспениваете молоко, а индикатор пароварки показывает 0,063 унции. воды было использовано в процессе. Вам нужно добавить 2 унции. эспрессо плюс 7 унций. молоко плюс 0,063 унции. пара. Но поскольку это лабораторное задание по химии, вам придется выполнять расчеты со значащими цифрами.
Просмотрев правила сложения и вычитания со значащими цифрами, найдите место последней значащей цифры вашего наименее определенного числа . Ваше молоко и эспрессо имеют объем по одной значащей цифре, занимая место .
Добавление объемов жидкости в вашем латте:
7 унций.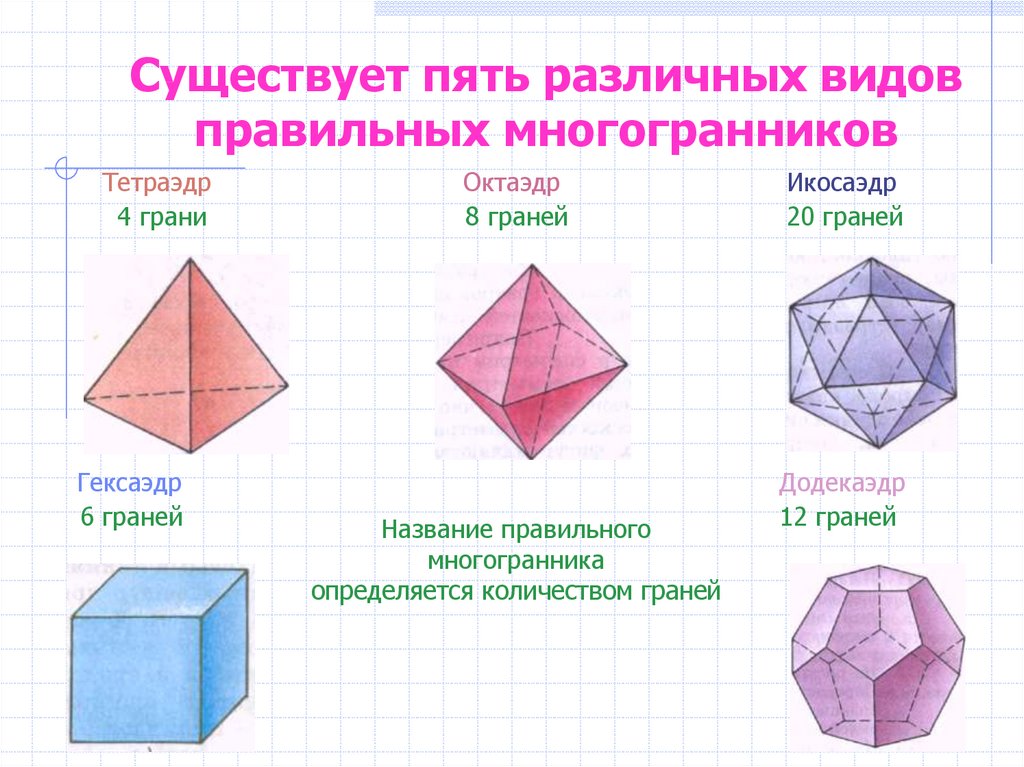 молоко + 2 ст. эспрессо + 0,063 унции. вода = 9,063 унции.
молоко + 2 ст. эспрессо + 0,063 унции. вода = 9,063 унции.
9,063 унции. округлить до единиц = 9 унций.
Несмотря на то, что у вас есть объем жидкости, который кажется точным до тысячных, вы должны округлить до единиц, потому что это наименее значимое разрядное значение. Итак, следуя правилам сложения со значащими цифрами, вы сообщаете, что ваш латте равен 9.унция в объеме.
Правила умножения и деления со значащими цифрами
- Для каждого числа в вашем расчете найдите количество значащих цифр
- Умножайте и/или делите числа в своих вычислениях, как обычно
- Округлите ответ до наименьшего количества значащих цифр, которое вы нашли на шаге 1
Пример: умножение и деление со значащими цифрами
Словесная задача на тесте по физике звучит так: Морские ученые определили уникального кита, который кричит с частотой 52 герца. Мы знаем, что звук распространяется по воздуху со скоростью около 343 метров в секунду. Учитывая, что звук скорости распространяется в воде в 4,3148688 раз быстрее, чем в воздухе, какова длина волны крика кита на частоте 52 Гц?
Формула для длины волны:
\( \lambda = \dfrac{v}{f} \)
Где
\( \лямбда \) = длина волны в метрах
\( v \) = скорость в метрах в секунду
\( f \) = частота в герцах
Итак, длина волны равна скорости, деленной на частоту. Для этой физической задачи вам нужно умножить скорость звука в воздухе на 4,3148688, чтобы получить скорость звука в воде. Затем разделите это число на 52 Гц, чтобы получить длину волны звуковой волны.
Для этой физической задачи вам нужно умножить скорость звука в воздухе на 4,3148688, чтобы получить скорость звука в воде. Затем разделите это число на 52 Гц, чтобы получить длину волны звуковой волны.
- \( \lambda = \dfrac{v}{f} \)
- \( \lambda = \dfrac{343 \times 4.3148688}{52} \)
- \( \lambda = \dfrac{ 1480}{52}\)
- \(\лямбда = 28,4615384\) метров
Следуя правилам умножения и деления со значащими цифрами, вы должны округлить окончательный ответ до наименьшего количества значащих цифр, учитывая исходные числа. В этом случае 52 имеет наименьшее количество значащих цифр, поэтому вы должны округлить окончательный ответ до 2 цифр.
28,4615384 метра, округленное до 2 знаков = 28 метров. Таким образом, в воде одна длина волны крика кита с частотой 52 Гц составляет 28 метров.
Примечание. Выполнение математических операций со значащими цифрами
Если вы вводите постоянное или точное значение, которое может встречаться в формуле, обязательно укажите правильное количество значащих цифр.
Например, рассмотрим формулу диаметра круга d = 2r, где диаметр в два раза больше длины радиуса. Если вы измерили радиус 2,35, умножьте на 2, чтобы найти диаметр круга: 2 * 2,35 = 4,70
Если вы используете этот калькулятор для расчетов и введете только «2» в качестве константы множителя, калькулятор будет читать 2 как одну значащую цифру. Ваш результирующий расчет будет округлен от 4,70 до 5, что явно не является правильным ответом на расчет диаметра d=2r.
Вы можете думать, что константы или точные значения имеют бесконечно много значащих цифр или, по крайней мере, столько значащих цифр, сколько наименее точное число в вашем вычислении. В этом примере вам нужно ввести 2,00 в качестве константы множителя, чтобы она имела то же количество значащих цифр, что и запись радиуса. Полученный ответ будет 4,70, который имеет 3 значащих цифры.
Связанные калькуляторы
Чтобы узнать больше об округлении значащих цифр, см.
Калькулятор округления значащих цифр.
Для получения дополнительной информации об округлении чисел в целом см. наш Калькулятор округления чисел.
Чтобы попрактиковаться в определении значащих цифр в числах, см.
Счетчик значимых цифр.
Ссылки
- Хан, Салман «Важные фигуры»
Академия Хана . - Вайсштейн, Эрик В. «Значимые цифры»,
MathWorld — Веб-ресурс Wolfram.
Определение, типы, список, решенные примеры, факты
Что такое фигуры?
В геометрии форму можно определить как форму объекта или его контур, внешнюю границу или внешнюю поверхность.
Все, что мы видим в окружающем нас мире, имеет форму. Мы можем найти различные основные формы, такие как двухмерный квадрат, прямоугольник и овал или трехмерную прямоугольную призму, цилиндр и сферу, в объектах, которые мы видим вокруг нас. Эти геометрические формы появляются в объектах, которые мы видим, таких как кредитные карты, банкноты и монеты, перстни, фоторамки, доски для игры в дартс, хижины, окна, волшебные палочки, высокие здания, цветочные горшки, игрушечные поезда и воздушные шары.
Эти геометрические формы появляются в объектах, которые мы видим, таких как кредитные карты, банкноты и монеты, перстни, фоторамки, доски для игры в дартс, хижины, окна, волшебные палочки, высокие здания, цветочные горшки, игрушечные поезда и воздушные шары.
Связанные игры
Различные типы фигур
Фигуры можно разделить на открытые и замкнутые.
| В геометрии незамкнутая форма может быть определена как форма или фигура, сегменты линий и/или кривые 90 105 которых не пересекаются. Они не начинаются и не заканчиваются в одной и той же точке. | В геометрии замкнутая форма может быть определена как замкнутая фигура или фигура, сегменты линий и/или кривые которых соединены или пересекаются. Они начинаются и заканчиваются в одной и той же точке. |
Замкнутые геометрические формы можно разделить на две большие категории, а именно двухмерные формы и трехмерные формы.
Плоская двухмерная форма. | Трехмерная фигура — это сплошная фигура. |
| Он имеет два измерения, то есть длину и ширину. | Он имеет два измерения: длину, ширину и глубину. |
Вот список двухмерных или двухмерных фигур с их названиями и изображениями:
| Двумерные геометрические фигуры |
Вот список трехмерных или трехмерных фигур с их названиями и изображениями: Геометрические фигуры
Цвет, общий размер и ориентация, называемые неопределяющими атрибутами двухмерной или трехмерной формы, никак не определяют форму и не влияют на нее. Эти атрибуты могут изменяться без какого-либо влияния на форму.
С другой стороны, определяя такие атрибуты, как количество сторон (параллельных или непараллельных, прямых или изогнутых), вершин, ребер и граней формы, открытость формы или замкнутость, а также меры углов определяют форма двухмерного или трехмерного объекта.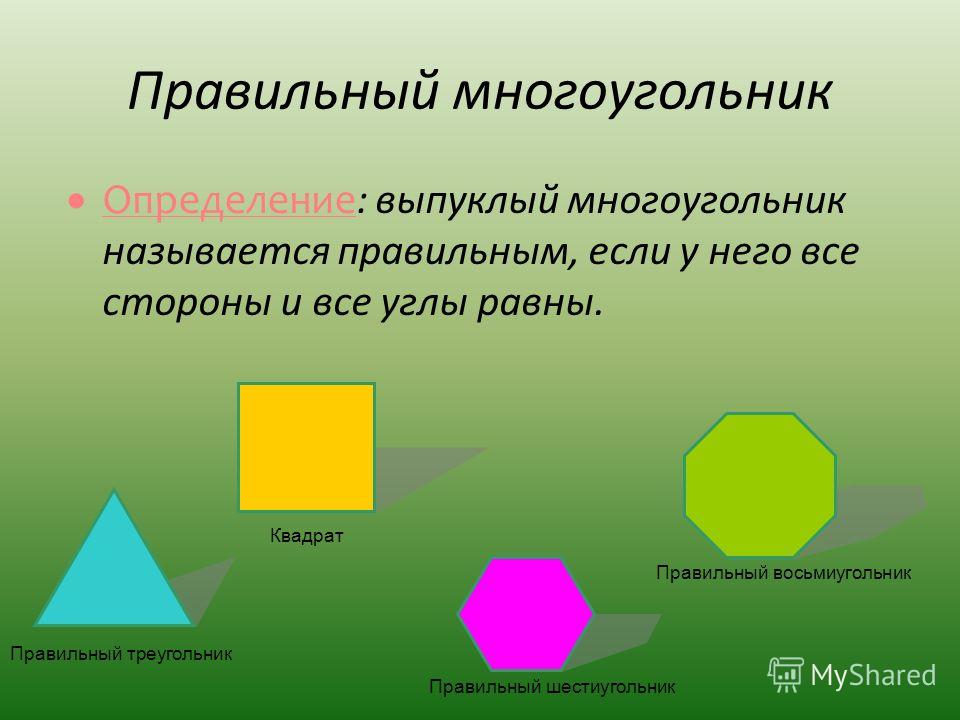 Любое изменение этих определяющих атрибутов изменит форму.
Любое изменение этих определяющих атрибутов изменит форму.
Связанные рабочие листы
Решенные примеры фигур
Пример 1. Назовите фигуры.
- Многоугольник с 6 сторонами.
- Контур двери.
- При складывании квадрата угол в угол.
- Квадрат и треугольник поверх него.
Решение:
- Шестиугольник
- Прямоугольник или четырехугольник
- Треугольник
- Пентагон
Пример 2: Классифицируйте данные буквы как открытые или закрытые.
C, D, L, M, O, S, U, V, Z
Решение:
Открытая форма: C, L, M, S, U, V, Z
Закрытая форма: D, O
Пример 3. Определить объемную форму данных объектов.
- Глобус
- Книга
- Банка для холодных напитков
- Кости
Решение:
- Сфера
- Прямоугольный
- Цилиндр
- Куб
Пример 4.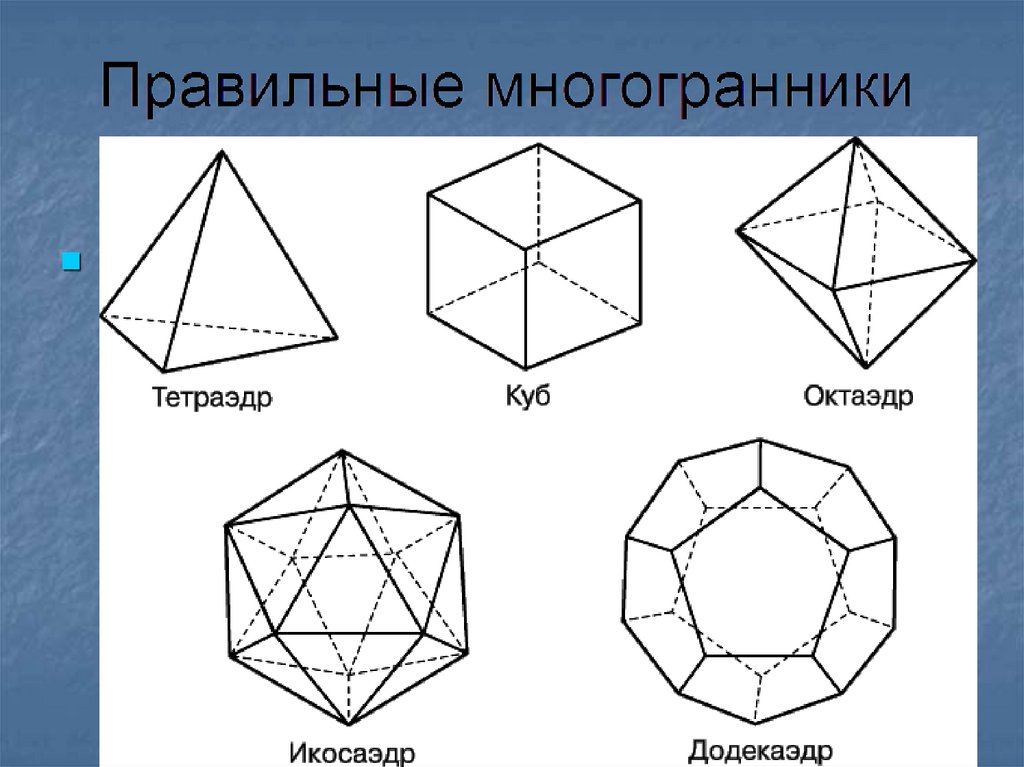 Почему луна в форме полумесяца не является многоугольником?
Почему луна в форме полумесяца не является многоугольником?
Решение:
Луна в форме полумесяца не является многоугольником, поскольку имеет изогнутые линии.
Практические задачи на фигурах
1
Как называется восьмиугольник?
шестиугольник
семиугольник
восьмиугольник
четырехугольник
Правильный ответ: восьмиугольник
Многоугольник с 8 сторонами известен как восьмиугольник.
2
Сколько измерений имеет твердое тело?
1
2
3
зависит от формы
Правильный ответ: 3
Все объемные формы являются трехмерными.
3
Какое из следующих утверждений неверно?
замкнутые формы могут иметь только прямые стороны.
замкнутые формы имеют определенную площадь.
начальная и конечная точки замкнутой формы совпадают.