Равнобедренная трапеция — это вид трапеции с равными боковыми сторонами.
Также встречаются такие названия, как равнобокая или равнобочная.
Прямоугольная трапеция — это трапеция, у которой углы при боковой стороне прямые.
a, b — основания трапеции (a параллельно b),
m, n — боковые стороны трапеции,
d1, d2 — диагонали трапеции,
h — высота трапеции (отрезок, соединяющий основания и при этом перпендикулярен им),
MN — средняя линия (отрезок, соединяющий середины боковых сторон).
Средняя линия параллельна основаниям, равна их полусумме и разделяет каждый отрезок с концами, находящимися на прямых, которые содержат основания, (к примеру, высоту фигуры) пополам:
MN || a, MN || b, MN = \frac{a + b}{2}
Сумма углов трапеции, прилежащих к каждой боковой стороне, равна 180^{\circ}:
\alpha + \beta = 180^{\circ}
\gamma + \delta =180^{\circ}
Равновеликими, то есть имеющими равные площади, являются отрезки диагоналей и треугольники AOB и DOC, образованные боковыми сторонами.
Подобными треугольниками являются AOD и COB, которые образованы своими основаниями и отрезками диагоналей.
\triangle AOD \sim \triangle COB
Коэффициент подобия k находится по формуле:
k = \frac{AD}{BC}
Причем отношение площадей этих треугольников равно k^{2}.
Каждый отрезок, соединяющий основания и проходящий через точку пересечения диагоналей трапеции, поделен этой точкой в отношении:
\frac{OX}{OY} = \frac{BC}{AD}
Это будет являться справедливым и для высоты с самими диагоналями.
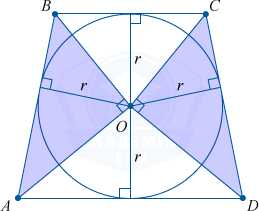
Каждая равнобокая трапеция может содержать описанную окружность. Только равнобокую трапецию возможно вписать в окружность.
Треугольники AOB и DOC являются прямоугольными, если трапеция ABCD описана около окружности. Центром же вписанной окружности будет являться точка O.
Опущенные на гипотенузы, высоты этих треугольников, тождественны радиусу вписанной окружности, а высота трапеции тождественна диаметру вписанной окружности.
academyege.ru
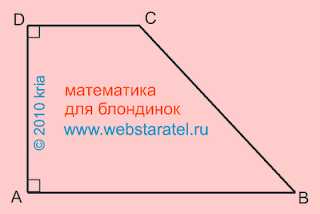У прямоугольной трапеции всегда есть два прямых угла. На рисунке прямые углы обозначены маленькими квадратиками в вершинах А и D. Прямые углы могут располагаться в двух любых смежных вершинах трапеции.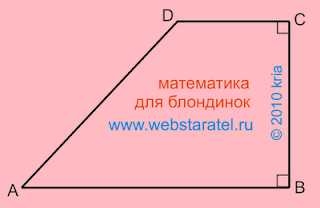 
На этом рисунке прямоугольной трапеции прямые углы расположены в вершинах В и С.
В математике существует определение прямоугольной трапеции, которое приведено и в Википедии: прямоугольной называется трапеция, у которой хотя бы один угол прямой. Это классическое определение прямоугольной трапеции, тупо переписанное из священных математических книг. В Евклидовой геометрии прямоугольная трапеция всегда имеет два прямых угла, поскольку две стороны трапеции, называемые основаниями, параллельны. Отрезок ВС, образующий прямой угол с основанием АВ, будет всегда перпендикулярен второму основанию CD. С одним или тремя прямыми углами может быть только криволинейная прямоугольная трапеция, а это уже совсем другой другой класс геометрических фигур.
Для блондинок помогала рисовать kria, автор блога kria-tiv.Помимо геометрической прямоугольной трапеции бывает ещё трапеция в цирке - это такая перекладина на веревочках, которая с потолка свисает. На таких трапециях воздушные акробаты катаются. Но прежде, чем в цирке залезать на трапецию, нужно взять абонемент в фитнес клуб в Уфе и усиленно позаниматься. Если вы живете в другом городе, там такие фитнес клубы тоже есть. Пусть вы не станете воздушной гимнасткой, но выглядеть будете стройной и красивой, а не как прямоугольная трапеция :)))
www.webstaratel.ru
Что такое прямоугольная трапеция и какими свойствами она обладает?
Определение.
Прямоугольная трапеция — это трапеция, у которой одна боковая сторона перпендикулярна основаниям.
Рисунок прямоугольной трапеции
ABCD- прямоугольная трапеция,
AD ∥ BC — основания трапеции,
AB и CD — ее боковые стороны,
Свойства прямоугольной трапеции:
1) Высота прямоугольной трапеции равна ее меньшей боковой стороне.
AB — высота трапеции ABCD.
2) У прямоугольной трапеции два угла — прямые, один — острый и один — тупой.
∠A и ∠B — прямые, ∠D — острый, ∠C — тупой.
3) Высота, проведенная из вершины тупого угла, делит прямоугольную трапецию на прямоугольник и прямоугольный треугольник.
ABCD — прямоугольник (так как у него все углы — прямые). Следовательно, AF=BC, CF=AB.
FCD — прямоугольный треугольник. FD=AD-AF,
отсюда FD=AD-BC. Если AD=a, BC=b, CF=AB=h, то
и по теореме Пифагора
4) Квадрат меньшей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и меньшего основания.
Треугольник ABC — прямоугольный.
По теореме Пифагора,
5) Квадрат большей диагонали прямоугольной трапеции равен сумме квадратов ее высоты и большего основания.
Треугольник ABD — прямоугольный.
По теореме Пифагора,
www.treugolniki.ru
Что такое равнобедренная трапеция и каковы ее свойства?
Определение.
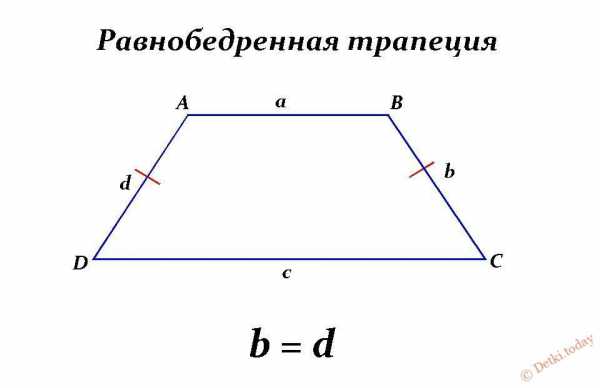
Равнобедренная трапеция — это трапеция, у которой боковые стороны равны.
Еще равнобедренную трапецию называют равнобокой (или равнобочной) трапецией.
рисунокравнобедреннойтрапеции
ABCD — равнобедренная трапеция.
AD и BC — основания трапеции,
AB и CD — её боковые стороны,
AB=CD.
Перечислим основные свойства равнобедренной трапеции.
Свойства равнобедренной трапеции:
1) Углы при основании равнобедренной трапеции равны.
∠A=∠D, ∠B=∠C
2) Сумма противолежащих углов равнобедренной трапеции равна 180º.
∠A+∠C=180º, ∠B+∠D=180º
3) Диагонали равнобедренной трапеции равны.
AC=BD
4) Около любой равнобедренной трапеции можно описать окружность.
Кроме основных, у равнобедренной трапеции есть и другие свойства. Например, можно доказать один раз и в дальнейшем использовать при решении задач следующее утверждение:
Высота, опущенная из вершины на большее основание, делит его на два отрезка, один из которых равен полусумме оснований, а другой — полуразности оснований.
AD=a, BC=b
Признаки равнобедренной трапеции:
1) Если углы при основании трапеции равны, то она — равнобедренная.
2) Если сумма противолежащих углов трапеции равна 180º, то она — равнобедренная.
3) Если диагонали трапеции равны, то она — равнобедренная.
4) Если около трапеции можно описать окружность, то она — равнобедренная.
www.treugolniki.ru
Трапеция – четырехугольник у которого две стороны параллельны. Параллельные стороны – это основание, непараллельные стороны – боковые.
Существует несколько основных видов: криволинейная, равнобедренная, произвольная, прямоугольная. Вычисления площади трапеции по формуле разнятся в зависимости от конкретного типа геометрической фигуры.
Содержание:
Всего существует четыре типа, отличающихся между собой не только вариативностью углов, но и возможным наличием криволинейных отрезков.
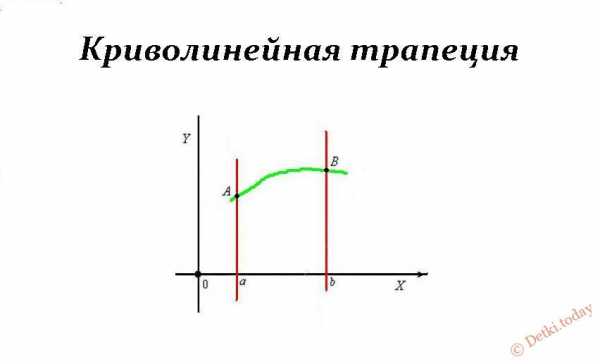
Вариативность расчета площади произвольной трапеции невелика. Ее можно вычислить относительно заданных размеров основания и высоты; посчитать через обозначенные четыре стороны фигуры; решить пример, зная длину средней линии и высоты; по указанным диагоналям и углом между ними; высчитать через основания и два угла.
Основная формула расчета данного способа: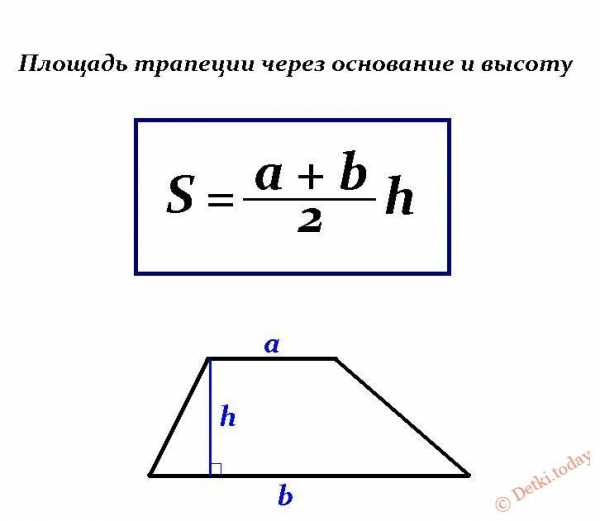
Где а и b – параллельные стороны, а h – высота четырехугольника.
Пример задачи: Дана плоская геометрическая фигура, параллельные стороны которой соответствуют длине 12 и 20 см, а высота равна – 10 см. Как найти площадь?
Решение: Допустимое решение согласно вышеприведенной формуле S = (a + b)/2 x h: S = (12 + 20)/2 x 10 = 160 см².
Зная длину средней линии и высоту плоской фигуры, всегда можно найти площадь трапеции, выполнив буквально одно действие:
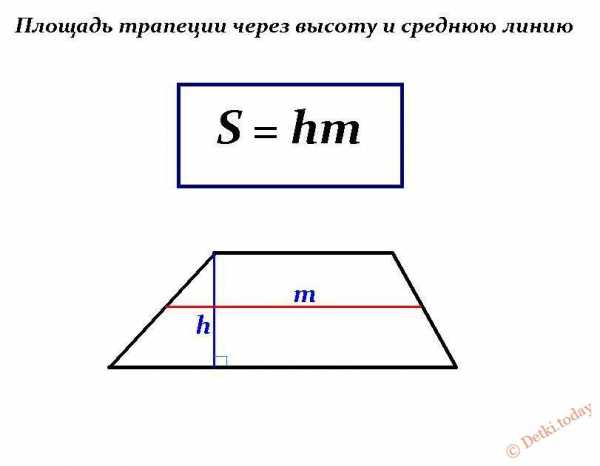Где h – высота четырехугольника, а m – средняя линия (прямая, соединяющая середины боковых сторон).
Пример решения задачи: Дана трапеция, в которой длина средней линии – 28 см, а высота фигуры – 19 см. Какова площадь плоского четырехугольника?
Решение: Используя формулу S = hm, подставляем вместо букв цифровые значения из условия задачки. Получаем S = 28 х 19 = 532 см².
Этот метод не так прост, как предыдущие. Здесь взяты за основу основные теоремы геометрии, а потому принцип расчета площади трапеции выглядит следующим образом:
Где a, b, c, d – четыре стороны фигуры, причем сторона b в обязательном порядке должна быть длинней а.
Пример вычисления: Даны стороны – a = 2 см, b = 4 см, c = 8 см, d = 7 см. Как найти площадь трапеции?
Расчет: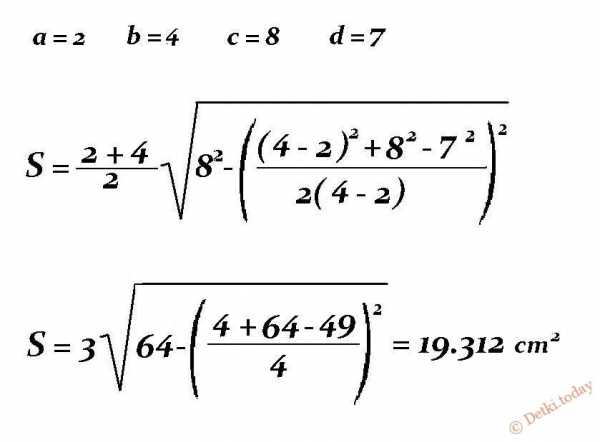
Вычислить площадь трапеции также можно, зная размеры обеих диагоналей и значения угла между ними.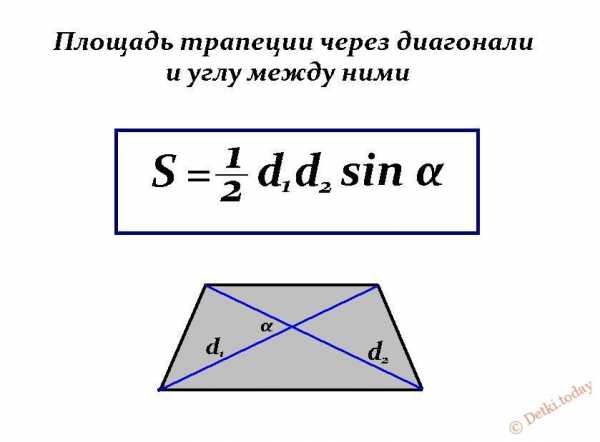
Обозначения: d₁ и d₂ — первая и вторая диагонали, α – угол между диагоналями.
Пример: Вычислить площадь фигуры при следующих известных значениях — d₁ = 17 см, d₂ = 25 см, α = 35⁰.
Верное решение: S = ½ х 17 х 25 х sin35 = 212,5 х 0,57 = 121,125 см².
Еще один вариант вычисления, основанный на расчете площади трапеции посредством длин двух оснований и двух углов.
Значения букв: b, a – длины оснований, α и β – углы.
Как посчитать (пример): Пускай угол α будет равен 67⁰, угол β = 106⁰, длина основания а равно 8 см, размер b = 11 см.
Решение: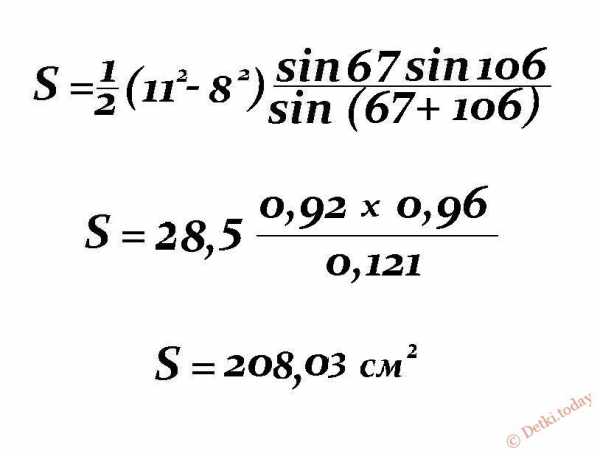
Отличным подспорьем в изучении основных типов вычислений площади являются видеоматериалы с доступным, легким языком изложения, подробными объяснениями и примерами решения задач.
Видео для новичков – доходчиво изложенная информация, содержащая основные формулы вычисления площади трапеции.
Видео содержит максимально полную информацию о видах трапеций, правильных буквенных обозначениях и вариантах решений разноплановых задач при помощи всех известных методов и принципов расчета.
Все перечисленные формулы и способы вычисления широко применимы во время изучения геометрии в школах и ВУЗах. Студенту, школьнику и абитуриенту предоставленная информация пригодится в качестве онлайн шпаргалки в период интенсивной подготовки к экзаменам, контрольным работам, написания рефератов, курсовых и подобных работ.
detki.today
Трапе́ция (от др.-греч. τραπέζιον — «столик»; τράπεζα — «стол, еда») — четырёхугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна). Две параллельные стороны называются основанием трапеции, а две другие — это боковые стороны. Иногда трапеция определяется как четырёхугольник, у которого пара противолежащих сторон параллельна (про другую не уточняется), в этом случае параллелограмм является частным случаем трапеции. В частности, существует понятие криволинейная трапеция.
Прямоугольная трапеция 
Равнобедренная трапеция ɴʙ Эти формулы — одинаковы, так как полусумма оснований равняется средней линии трапеции:
dic.academic.ru
Трапеция – четырехугольник, у которого только одна пара сторон параллельна (а другая пара сторон не параллельна).
Параллельные стороны трапеции называются основаниями. Другие две — боковые стороны.Если боковые стороны равны, трапеция называется равнобедренной.
Трапеция, у которой есть прямые углы при боковой стороне, называется прямоугольной.
Отрезок, соединяющий середины боковых сторон, называется средней линией трапеции.
1. Средняя линия трапеции параллельна основаниям и равна их полусумме.
2. Биссектриса любого угла трапеции отсекает на её основании (или продолжении) отрезок, равный боковой стороне.
3. Треугольники и , образованные отрезками диагоналей и основаниями трапеции, подобны.
Коэффициент подобия –
Отношение площадей этих треугольников есть .
4. Треугольники и , образованные отрезками диагоналей и боковыми сторонами трапеции, имеют одинаковую площадь.
5. В трапецию можно вписать окружность, если сумма оснований трапеции равна сумме её боковых сторон.
6. Отрезок, соединяющий середины диагоналей, равен полуразности оснований и лежит на средней линии.
7. Точка пересечения диагоналей трапеции, точка пересечения продолжений её боковых сторон и середины оснований лежат на одной прямой.
8. Если сумма углов при любом основании трапеции равна 90°, то отрезок, соединяющий середины оснований, равен их полуразности.
1. В равнобедренной трапеции углы при любом основании равны.
2. В равнобедренной трапеции длины диагоналей равны.
3. Если трапецию можно вписать в окружность, то трапеция – равнобедренная.
4. Около равнобедренной трапеции можно описать окружность.
5. Если в равнобедренной трапеции диагонали перпендикулярны, то высота равна полусумме оснований.
Если в трапецию вписана окружность с радиусом и она делит боковую сторону точкой касания на два отрезка — и , то
или где – средняя линия
Смотрите хорошую подборку задач с трапецией (входят в ГИА и часть В ЕГЭ) здесь и здесь.
Смотрите также площадь трапеции.
egemaximum.ru
